Paris

                                             RELACION Y FUNCION

RELACION: es una correspondencia entre dos conjuntos de elementos. el primer conjunto de elementos se llama dominio y el segundo rango

FUNCION:  es una relación donde a cada valor del primer conjunto, le corresponde un solo valor del segundo conjunto

ejemplo de relación con sus diferentes representaciones:

PROBLEMA: si una llave de agua alimenta a un tanque con un gasto de 8.5lts/min

a)¿existe una relación entre el volumen y el tiempo?

b)elabora una tabla para el volumen de agua suministrando en el intervalo de tiempo

c)construye la grafica de esta relación en el intervalo dado

SOLUCION:

a)si, existe una relación entre el tiempo y el volumen

b) la tabla para un intervalo seria

tiempo   0     1      2      3        4

volumen 0   8.5   17    25.5    34

                                      CRITERIO DE LA RECTA VERTICAL

“una curva es la grafica de una función si y solo si al trazar rectas verticales sobre ella, ninguna de ellas la intercepta en mas de un solo punto a la vez”

Regla de Correspondencia

Una correspondencia unívoca es una correspondencia matemática donde cada elemento del conjunto dominio se corresponde con solo un elemento del conjunto rango.

Una correspondencia biunívoca es simplemente una correspondencia univoca cuya correspondencia inversa también es unívoca. Es decir: cada elemento del primer conjunto se corresponde con solo un elemento del segundo conjunto, y cada elemento del segundo conjunto se corresponde con solo un elemento del primer conjunto.

DOMINIO, ARGUMENTO, IMAGEN Y CONTRADOMINIO

El dominio de una función es el primer conjunto de datos, sus elementos tienen su imagen en el contradominio

El argumento es cualquier elemento del dominio

La imagen es el elemento que le corresponde a un argumento de forma particular

El contradominio de una función es el segundo conjunto de datos, contiene a las imágenes

El rango esta conformado por el conjunto de imágenes, algunas veces es igual al contradominio

Una variable representa a aquello que esta sujeto a algún tipo de cambio, como la edad de una persona, la velocidad de un automóvil, etc.

Una forma de simbolizar una función es la siguiente:

F: A →B

EJERCICIOS

Para la función f definida por  f(x)=x2+4x+4, calcular:
F (2)

      F (-1)
      F (3ª)

SOLUCION

   F(2)=22+4(2)+4=16

   F(-1)=(-1)2+4(-1)+4=1

   F(3ª)=(3ª)2+4(3ª)+4

    F(b-3)=b2-2b+1

OPERACIONES CON FUNCIONES

Suma de funciones

Sean f y g dos funciones reales de variable real definidas en un mismo intervalo. Se llama suma de ambas funciones, y se representa por f + g, a la función definida por

(f + g)(x) = f(x) + g(x)

Resta de funciones

Del mismo modo que se ha definido la suma de funciones, se define la resta de dos funciones reales de variable real f y g, como la función

(f - g)(x) = f(x) - g(x)

Para que esto sea posible es necesario que f y g estén definidas en un mismo intervalo.

Producto de funciones

Sean f y g dos funciones reales de variable real, y definidas en un mismo intervalo. Se llama función producto de f y g a la función definida por

(f.g)(x) = f(x).g(x)

Cociente de funciones

Dadas dos funciones reales de variable real, f y g, y definidas en un mismo intervalo, se llama función cociente de f y g a la función definida por

(f/g)(x) = f(x)/g(x)

EJERCICIO

En una tienda de ropa se ofrece una camisa con descuento de 20% sobre el precio se lista. El impuesto a pagar por una prenda es de 16% si llamamos P(x) al importe a pagar con descuento e I(x) al impuesto a pagar.

Encuentra
I(x)o P(x)

B) P(x)+ I(x) o P(x)

Solución:
Si lo que hay que pagar con descuento por x camisas compradas es P(x)=x-0.2x y lo que hay que pagar de impuesto es I(x)=0.16x

Por lo tanto,

                      I(x)o P(x)= I(P(x))

                                     =(x-0.2x)

                                     =0.16(x-0.2x)

                                     =0.16x(1-0.2)

                                     =0.16x(0.8)

Lo cual indica el impuesto a pagar sobre el precio del articulo después de haberse aplicado el descuento del 16%
   P(x)+I(x)oP(x)=x-0.2x  +   0.16x(0.8)

                        =x-0.2   +   0.128x

                        = 0.928x pago final

                                            CLASIFICACION DE FUNCIONES

Podemos clasificar las funciones de acuerdo a la forma de la ecuación que la representa, por su grafica y por su dominio y rango

Funciones algebraicas

• Funciones polinómicas: Son las funciones x → P(x), donde P es un polinomio en x, es decir una suma finita de potencias de x multiplicados por coeficientes reales.
• Función lineal: ax + b es un binomio del primer grado
• Función cuadrática: ax² + bx + c es un trinomio del segundo grado.
• Funciones racionales: Son funciones obtenidas al dividir una función polinomial por otra, no idénticamente nula.
• Función raíz

Funciones trascendentes

• Función exponencial: De la forma y = a^x
• Función logarítmica
• Funciones trigonométricas: seno, coseno, tangente, secante, cosecante, cotangente, inversas trigonométricas.
• Funciones hiperbólicas: seno hiperbólico, coseno hiperbólico, tangente hiperbólica.

Funciones continuas

Se presenta cuando la grafica de la funcion no tiene ningun corte o salto.

Funcion discontinua

Si la grafica de la funcion tiene algun corte o salto, entonces se considera que la funcion es discontinua.

Funcion creciente

Son aquellas en las que cuando los valores del dominio aumentan los del contradominio lo hacen por igual.

Funcion decreciente.

Esta presente si los elementos del dominio aumentan, entonces las imagenes correspondientes disminuyan.

                                     FUNCIONES CONTINUAS Y DISCONTINUAS

CLASIFICACION DE LAS FUNCIONES DE ACUERDO A LA RELACION ENTRE DOMINIO Y RANGO

Funcion inyectiva (uno-uno)

Una funcion es iyectiva si cada f(x) en el recorrido es la imagen de exactamente un solo elemento del dominio; es decir, de todos los pares (x,y) pertenecente a la funcion, las y no se repiten.

Funcion sobreyectiva

Son aquellas en las que la aplicacion es sobre todo en contradominio, es decir, cuando el conjunto imagen esto significa que cada elemento del contradominio tiene un origen.

Funciones biyectiva

 Se van a identificar cuando veamos que son al mismo tiempo inyectivas y sobreyectivas

                                          APLICACIONES DE FUNCIONES

EJERCICIO:

La tortillera Carmen ofrece el kilo de tortilla a sus clientes con un precio de $12

Escribe la expresión matematica que nos ayuda a obtener el importe Y a pagar por la cantidad X de tortillas vendidas
El ingreso obtenido para 2, 3, 4 y 5 kilos de tortilla

¿Cuántos kilos de tortilla habrá vendido la tortillería Carmen si se obuvo un ingreso de $120 $348 $720

SOLUCION

La expresión matematica en y=12x, el cual se trata de una función

El ingreso obtenido para 2,3,4 y 5 kilos de tortilla son:

F (2) = 12(2)=$4

F (3) = 12(3)=$36

F (4) = 12(4)=$48

F (5) = 12(5)=$60

Puesto que y=12x, tenemos que x=y/12

 Y=120                   y=348                    y=720

X=120/12=10kg    x=348/12=29kg     x=720/12=60kg

Función inyectiva, sobreyectiva y biyectiva

"Inyectivo, sobreyectivo y biyectivo" te dan información sobre el comportamiento de una función.

Puedes entender una función como una manera de conectar elementos de un conjunto "A" a los de otro conjunto "B":

"Injectivo" significa que cada elemento de "B" tiene como mucho uno de "A" al que corresponde (pero esto no nos dice que todos los elementos de "B" tengan alguno en "A").
"Sobreyectivo" significa que cada elemento de "B" tiene por lo menos uno de "A" (a lo mejor más de uno).
"Biyectivo" significa inyectivo y sobreyectivo a la vez. Así que hay una correspondencia perfecta "uno a uno" entre los elementos de los dos conjuntos.

PRUEBA DE LA RECTA HORIZONTAL PARA FUNCIONES INYECTIVAS

una recta horizontal corta en un solo punto la grafica de una función inyectica

EJERCICIO

determina si la función y = 2x es biyectiva

SOLUCION

al dibujar la grafica de la función y hacer que la corte una recta horizontal, se sabe que la función es inyectiva, ya que de acuerdo con la prueba de la recta horizontal, esta corta en un solo punto la grafica f(x) = 2x

                                                 FUNCION INVERSA

Dada una función , se llama función inversa de y se denota por a otra función que para cualquier valor del dominio de se cumple que:
 

 
No todas las funciones tienen inversa, para que exista se tiene que cumplir que para cada valor del recorrido de f , proviene de un único valor del dominio .
Las gráficas de una función y su inversa son simétricas con respecto a la recta y=x


Para calcular la función inversa:

a) Se cambian los nombres de e .

b) Se despeja la .

Ejemplo

Calcula la inversa de la función .
Primero intercambiamos la y la : y después despejamos la :
 

 
Luego la función inversa de  es .
Vamos a comprobar que efectivamente es la inversa:
 

 
 

 
 

 Ejercicios

1. Comprueba que las funciones y son inversas.
2. Calcula la inversa de:

a)
b)

FUNCIÓN CONSTANTE 

Se llama función constante a aquella función constante que toma el mismo valor para cualquier valor de la variable independiente. Se la representa de la forma:

La función constante
Consideremos la función más sencilla, por ejemplo .
La imagen de cualquier número es siempre 2. Si
hacemos una tabla de valores tendríamos:


x -2 -1 0 1 2
y 2 2 2 2 2


Por tanto si representamos todos esos valores, y más que podríamos calcular, todos están en el 2 y la
gráfica resulta una línea recta que corta al eje de ordenadas en el punto 2
En general una función constante es una función cuya fórmula es Y=K donde k es un númeroreal. Su representación gráfica es una línea recta que corta al eje de ordenadas en el punto k.

FUNCION IDENTIDAD

Una función identidad es una función matemática, de un conjunto M a sí mismo, que devuelve su propio argumento.
La función de en tiene como representación gráfica en el eje de coordenadas la línea recta que cruza el origen subiendo en un ángulo de 45° hacia la derecha.
La función identidad en (el plano de los reales tomando las coordenadas polares) es la función determinada por la ecuación : una espiral que se aleja del origen uniformemente en el sentido contrario a las agujas del reloj.
La función identidad en es la doble negación, expresada por Fx

FUNCIÓN ESCALÓN 

En ingeniería es común encontrar funciones que corresponden a estados de sí o no, o bienactivo o inactivo. Por ejemplo, una fuerza externa que actúa sobre un sistema mecánico o una tensión eléctrica aplicada a un circuito, puede tener que suspenderse después de cierto tiempo. Para tratar de forma efectiva con estas funciones discontinuas conviene introducir una función especial llamada función escalón unitario.

Definición [Función de Heaviside]

La función escalón unitario o función de Heaviside  se define como

Observación: la función de heaviside se definio sobre el intervalo , pues esto es suficiente para la transformada de Laplace. En un sentido más general para . 

Ejemplo 

Trazar la gráfica de la función .

Solución 

La función está dada por

y su gráfica se muestra en la figura 

Cuando la función de Heaviside se multilplica por una función , definida para , ésta función se desactiva en el intervalo , como muestra en siguiente ejemplo.

Ejemplo 

Trazar la gráfica de la función .

Solución 

La función está dada por

La función de Heaviside puede utilizarse para expresar funciones continuas a trozos de una manera compacta, como se muestra en el siguiente ejemplo.

Ejemplo 

Use la función de Heaviside para reescribir la función

Solución 

Para reescribir la función basta usar la definición de la función Heaveside

Observación: la función

se escribe usando la función de Heaviside como

FUNCION VALOR ABSOLUTO 

Recordemos que la definición del valor absoluto surge de nociones geométricas, y se relaciona con los conceptos de longitud y distancia.

La función de valor absoluto tiene por ecuación f(x) = |x|, y siempre representa distancias; por lo tanto, siempre será positiva o nula.

En esta condición, de ser siempre positiva o nula, su gráfica no se encontrará jamás debajo del eje x. Su gráfica va a estar siempre por encima de dicho eje o, a lo sumo, tocándolo.

Las funciones en valor absoluto siempre representan una distancia o intervalos (tramos o trozos) y se pueden resolver o calcular siguiendo los siguientes pasos:

1. Se iguala a cero la función, sin el valor absoluto, y se calculan sus raíces (los valores de x).

2. Se forman intervalos con las raíces (los valores de x) y se evalúa el signo de cada intervalo.

3. Definimos la función a intervalos, teniendo en cuenta que en los intervalos donde la x es negativa se cambia el signo de la función.

4. Representamos la función resultante.

Veamos un ejemplo:








Otro ejemplo:









-----------------------------------------------------------------------------------------------------

FUNCION POLINOMIAL

¿Qué es una función polinomial?

Esto depende de los grados de la función. La función polinomial tiene relación con la expresión polinomial o con el polinomio. Si una expresión tiene muchos términos la función polinomial puede tenerlos o no, pero responde a la forma:

P(x)= anxn+an-1xn-1+an-2xn-2+…. + a0x0

Con la nota específica de que N es un nuero real y el coeficiente A no debe ser cero.

La función afín: FUNCIÓN POLINÓMICA DE GRADO 1 que tiene en su variable equis el exponente uno.

La forma de esta función de grado uno es la ecuación de la línea recta, que tiene su gráfica como aparece de forma oblicua.

y = m x + b



La función cuadrática:

FUNCIÓN POLINÓMICA DE GRADO 2

Se denomina función cuadrática a toda función de la forma:

Y = ax2+ bx+ c que representa a una expresión cuadrática, donde a (distinto de 0), b y c son números reales.

Su gráfica es una parábola.



La función cúbica:

FUNCIÓN POLINÓMICA DE GRADO 3

Se denomina función cúbica a toda función de la forma:

y= ax3 + bx2 + cx+ d; donde a (distinto de 0), b, c y d son números reales.



FUNCIÓN POLINÓMICA DE GRADO 4

Es la función de fórmula: y = ax4+ bx3+ cx2+ dx+ e; donde a (distinto de 0), b, c, d y e son números reales.

FUNCION LINEAL

En geometría y el álgebra elemental, una función lineal es una función polinómica de primer grado; es decir, una función cuya representación en el plano cartesiano es una línea recta. Esta función se puede escribir como:

donde m y b son constantes reales y x es una variable real. La constante m es la pendiente de la recta, y b es el punto de corte de la recta con el eje y. Si se modifica m entonces se modifica la inclinación de la recta, y si se modifica b, entonces la línea se desplazará hacia arriba o hacia abajo.
Algunos autores llaman función lineal a aquella con b= 0 de la forma:
mientras que llaman función afín a la que tiene la forma:
cuando b es distinto de cero.

Ejemplo

Una función lineal de una única variable dependiente x es de la forma:
que se conoce como ecuación de la recta en el plano x,y.
En la figura se ven dos rectas, que corresponden a las ecuaciones lineales siguientes:
en esta recta el parámetro m= 1/2 por tanto de pendiente 1/2, es decir, cuando aumentamos x en una unidad entonces y aumenta en 1/2 unidad, el valor de b es 2, luego la recta corta el eje y en el punto y= 2.
En la ecuación:
la pendiente de la recta es el parámetro m= -1, es decir, cuando el valor de x aumenta en una unidad, el valor de y disminuye en una unidad; el corte con el eje y es en y= 5, dado que el valor de b= 5.
En una recta el valor de m se corresponde al ángulo de inclinación de la recta con el eje de las x a través de la expresión:

Función cuadrática

En matemáticas, una función cuadrática o función de segundo grado es una función polinómica definida como:


en donde a, b y c son números reales (constantes) y a es distinto de 0.

La representación gráfica en el plano cartesiano de una función cuadrática es una parábola, cuyo eje de simetría es paralelo al eje de las ordenadas. La parábola se abrirá hacia arriba si el signo de a es positivo, y hacia abajo en caso contrario. El estudio de las funciones cuadráticas tiene numerosas aplicaciones en campos muy diversos, como por ejemplo la caída libre o el tiro parabólico.

La derivada de una función cuadrática es una función lineal y su integral una función cúbica.

gráficas de funciones cuadráticas

Raíces

Véase también: Ecuación de segundo grado.
Las raíces (o ceros) de una función cuadrática, como en toda función, son los valores de x, para los cuales . Por tratarse de un polinomio de grado 2, habrá a lo sumo 2 raíces, denotadas habitualmente como: y , dependiendo del valor del discriminante Δ definido como .Dos soluciones reales y diferentes si el discriminante es positivo:.Una solución real doble si el discriminante es cero:
Dos números complejos conjugados si el discriminante es negativo:

Representación analítica

Existen tres formas principales de escribir una función cuadrática, aplicables según el uso que se le quiera dar a la función: un estudio analítico de la función o de la ecuación cuadrática, una interpretación o construcción geométrica de la parábola, etc. Las tres formas son equivalentes.

Forma desarrollada

La forma desarrollada de una función cuadrática (o forma estándar) corresponde a la del polinomio de segundo grado, escrito convencionalmente como:
con .

Forma factorizada

Toda función cuadrática se puede escribir en forma factorizada en función de sus raíces como:
siendo a el coeficiente principal de la función, y y las raíces de . En el caso de que el discriminante Δ sea igual a 0 entonces por lo que la factorización adquiere la forma:
En este caso a se la denomina raíz doble, ya que su orden de multiplicidad es 2.

Forma canónica

Toda función cuadrática puede ser expresada mediante el cuadrado de un binomio de la siguiente manera:
siendo a el coeficiente principal y el par ordenado (h;k) las coordenadas del vértice de la parábola.

Representación gráfica

Corte con el eje y

La función corta el eje y en el punto y = f(0), es decir, la parábola corta el eje y cuando x vale cero (0):
lo que resulta:
la función corta el eje y en el punto (0, c), siendo c el término independiente de la función.
A este punto de la función también se lo conoce con Ordenada al Origen

Corte con el eje x

La función corta al eje x cuando y vale 0, dada la función:
se tiene que:
las distintas soluciones de esta ecuación de segundo grado, son los casos de corte con el eje x, que se obtienen, como es sabido, por la expresión:.
Si la función no corta al eje x, la fórmula anterior no tiene solución (en los reales).

Extremos

Toda función cuadrática posee un máximo o un mínimo, que es el vértice de la parábola. Si la parábola tiene concavidad hacia arriba, el vértice corresponde a un mínimo de la función; mientras que si la parábola tiene concavidad hacia abajo, el vértice será un máximo.
Dada la función en su forma desarrollada: , la coordenada x del vértice será simplemente: . La coordenada y del vértice corresponde a la función fevaluada en ese punto.
Dada la forma canónica: , las coordenadas explícitas del vértice son: (h,k).

FUNCIONES DE PRIMER GRADO Y MODELOS LINEALES

ECUACION DE PRIMER GRADO

Una ecuación de primer grado o ecuación lineal significa que es un planteamiento de igualdad, involucrando una o más variables a la primera potencia, que no contiene productos entre las variables, es decir, una ecuación que involucra solamente sumas y restas de una variable a laprimera potencia.

Modelos Lineales

Se dice que una función es lineal cuando su gráfica es una línea recta; y por consecuencia tiene la forma:
y = f(x) = mx + b
Donde m representa la pendiente de la recta y b la ordenada al origen (el punto en el que la recta interfecta al eje de las "y"). Es importante mencionar que este tipo de funciones crecen a tasa constante; y su dominio e imagen son todos los números reales.

FUNCIONES DE SEGUNDO GRADO Y MODELOS CUADRATICOS

Una ecuación de segundo grado1 2 o ecuación cuadrática es una ecuación que tiene la forma de una suma de términos cuyo grado máximo es dos, es decir, una ecuación cuadrática puede ser representada por un polinomino de segundo grado o polinomio cuadrático. La expresión canónica general de una ecuación cuadrática es:




donde x representa la variable y a, b y c son constantes; a es un coeficiente cuadrático (distinto de 0), b el coeficiente lineal y c es el término independiente. Este polinomio se puede representar mediante una gráfica de una función cuadrática o parábola. Esta representación gráfica es útil, porque la intersección de esta gráfica con el eje horizontal coinciden con las soluciones de la ecuación (y dado que pueden existir dos, una o ninguna intersección, esos pueden ser los números de soluciones de la ecuación).




Los puntos comunes de una parábola con el eje X (recta y = o), si los hubiese, son las soluciones reales de la ecuación cuadrática.

FUNCION POLINOMIAL DE GRADO TRES

Gráfica de una función cúbica del tipo y = K(x+4)·(x+1)·(x-2). Las raíces son los lugares donde la curva cruza el eje x (y = 0), esto es: x1 = -4, x2 = -1 y x3 = 2.

FUNCION CUBICA

La función cúbica es una función polinómica de tercergrado. Tiene la forma:

donde el coeficiente a es distinto de 0.

Tanto el dominio de definición como el conjunto imagen de estas funciones pertenecen a los números reales.

La derivada de una función cúbica genera una función cuadrática y su integral una función cuártica.

Ecuación cúbica

La ecuación cúbica es la ecuación que resulta de igualar a cero la función cúbica, y tiene la forma canónica:

donde a, b, c y d (a ≠ 0) son números que pertenecen a un campo, usualmente el campo de los números reales o el de los números complejos.

FUNCION POLINOMIAL DE GRADO CUATRO (FUNCION CUARTICA)

Gráfico de una ecuación de cuarto grado.

Ecuación de cuarto grado

Una ecuación de cuarto grado o ecuación cuártica con una incógnita es una ecuación que se puede poner bajo la forma canónica:

donde a, b, c, d y e (siendo ) son números que pertenecen a un cuerpo, usualmente a los reales o los complejos .

Caso general

Sea K un cuerpo, donde se pueden extraer raíces cuadradas y cúbicas (y por lo tanto también de cuarto orden, pues equivale a extraer raíces cuadradas dos veces seguidas). En este cuerpo, es posible factorizar por todo a, y la identidad siguiente es válida:.

En un cuerpo algebraicamente cerrado, se sabe que todo polinomio de grado 4 tiene cuatro raíces. Es el caso del cuerpo de los complejos, según el Teorema Fundamental del Álgebra.

El método siguiente permite obtener las cuatro raíces al mismo tiempo. Este método es llamado "método de Descartes", pues fue dado por el matemático francés René Descartes (1596-1650) en el año de 1637 en su célebre libro "La Geometría". Aunque existan diferentes métodos para resolver las ecuaciones cuárticas, algunos son: método de Ferrari, método de Descartes, método de Euler, método de Lagrange, método deAlcalá, etcétera.

Método de Descartes

Los pasos de la resolución para el método de Descartes (1637) son:
Dividir la ecuación inicial por el coeficiente a. Se obtiene:, donde , , y
Proceder al cambio de incógnita , para suprimir el término cúbico. En efecto, al desarrollar con la identidad precedente, vemos aparecer el término , compensado exactamente por que aparece en . Tras sustituir x y operando con las identidades notables, se obtiene:, con p, q y r números del cuerpo.
Y ahora, la idea genial: factorizar lo anterior en , lo que es posible porque no hay z³ en el polinomio.

Desarrollando la expresión e identificando los dos polinomios, obtenemos las condiciones: (coeficiente de x²) (coeficiente en x) (término constante)

Después de algunos cálculos, hallamos : Es una ecuación de sexto grado, pero si miramos bien, α sólo aparece con potencias pares.

Pongamos . Entonces:, que resulta ser una ecuación de tercer grado en la variable y que se puede resolver usando el método de Cardano.

Luego se encuentra α, β y γ, y se resuelven y , y para terminar, no olvide que .

FUNCIONES RACIONALES 

Función racional de grado 2:

Función racional de grado 3:

Una función racional es una función que puede ser expresada de la forma:




donde P y Q son polinomios y x una variable, siendo Q distinto del polinomio nulo. Las funciones racionales están definidas o tienen su dominio de definición en todos los valores de x que no anulen el denominador.1

La palabra "racional" hace referencia a que la función racional es una razón o cociente (de dos polinomios); los coeficientes de los polinomios pueden ser números racionales o no.

Las funciones racionales tienen diversas aplicaciones en el campo del análisis numérico para interpolar o aproximar los resultados de otras funciones más complejas, ya que son computacionalmente simples de calcular como los polinomios, pero permiten expresar una mayor variedad de comportamientos.

Ejemplos

Función homográfica:

si el denominador es distinto de cero, y si ad ≠ bc, la curva correspondiente es una hipérbola equilátera.2

Propiedades

-Toda función racional es de clase en un dominio que no incluya las raíces del polinomio Q(x).
-Todas las funciones racionales en las que el grado de Q sea mayor o igual que el grado de P tienen asíntotas (verticales, horizontales u oblicuas).

Raíces de la Función Racional

Una raíz a de una función racional f es el valor donde f(a)=0

Lo anterior significa que, para encontrar las raíces de la función polinómica f, tenemos que resolver la ecuaciónf(x)=0. Para que la función exista, el denominador debe ser distinto de cero. Por lo tanto para encontrar las raíces de la función polinómica fx= P(x)Q(x) , si P(x) y Q(x) no tienen factor comun, es suficiente resolverP(x)=0.

La raíz de una función racional fx= P(x)Q(x) es el valor donde el numerador, P(x)=0

Ejemplo 1:

Encontrar las raíces de la función f x = x 3 + x 2 - 2 x 2 x 2 - x - 6Solución:

Recordemos que el denominador no puede ser igual a cero. Por lo tanto, para encontrar las raíces de la función racional solo es necesario encontrar las raíces del numerador. Factorizando el numerador obtenemos:

f x = x x-1 x+2 2 x 2 - x - 6

Por lo tanto:


x = 0

o

x-1 = 0 x = 1

o

x+2 = 0 x = -2


Las raíces de la función f x = x 3 + 3 x 2 - 2 x 2 x 2 - x - 6 son x=0, x=1 y x=-2

Puedes visualizar estas raíces observando la gráfica de esta función, que es la siguiente:

Ejemplo 2:

Encontrar las raíces de la función f x = x 3 + 5 x 2 + 4 x x 2 + x - 2Solución:

Factorizando el numerador en la expresión obtenemos:

f x = x x+1 x+4 x 2 + x - 2

Como el denominador no puede ser igual a cero. La función puede ser cero si alguno de los factores del numerador es cero:


x = 0

o

x+1 = 0 x = -1

o

x+4 = 0 x = -4


Las raíces de la función f x = x 3 + 5 x 2 + 4 x x 2 + x - 2 son x=0, x=-1 y x=-4

Puedes visualizar estas raíces observando la gráfica de esta función, que es la siguiente:

Ejemplo 3:

Encontrar las raíces de la función f x = x 2 + 1 x - 1Solución:

Los ceros de la función racional son los ceros del numerador. Notemos que en este caso, el numerador no tiene ceros reales. Pues,

x 2 +1 = 0 x 2 = -1 x = ± - 1 x = ± i

Las raíces de la función f x = x 2 + 1 x - 1 son x=i y x=-i

La gráfica de esta función es la siguiente, como vemos la función no toca el eje x:

ASINTOTAS DE LA GRAFICA DE UNA FUNCION RACIONAL

Hemos visto que las raíces del numerador corresponden a las raíces de la función racional.

Una función racional, f, tiene una asíntota vértical en aquellos valores que hacen cero el denominador de la función que no hacen cero el numerador de la misma.Ilustremos esto mediante los siguientes ejemplos.

Ejemplo 1:

Considera la función f x = 1 x - 1 . Cómo se comporta la función cerca de las raíces del denominador?Solución:Igualando el denominador a cero para hallar sus raíces, obtenemos:x-1 = 0 x = 1




Vemos que cuando x se acerca a 1 por la izquierda el valor de la función decrece rápidamente. Cuando x se acerca a 1 por la derecha, el valor de la función crece rápidamente
Cuando x se acerca a una raíz del denominador, el valor del denominador disminuye acercándose a cero y el valor de la función crece con rapidez tendiendo hacia el infinito o disminuye con rapidez tendiendo hacia el infinito negativo.


Observa la gráfica de la función en los valores cercanos a x=1.



Ejemplo2:

Considera la función f x = 1 x-1 x-2 . Cómo se comporta la función cerca de las raíces del denominador?Solución:Igualando el denominador a cero para hallar sus raíces, 
obtenemos:


x - 1 = 0 x = 1
o
x - 2 = 0 x = 2



Vemos que cuando x se acerca a 1 por la izquierda el valor de la función crece rápidamente. Cuando x se acerca a 1 por la derecha, el valor de la función decrece rápidamente


Vemos que cuando x se acerca a 2 por la izquierda el valor de la función decrece rápidamente. Cuando x se acerca a 2 por la derecha, el valor de la función crece rápidamente

Observa la gráfica de la función en los valores cercanos a x=1 y x=2.

FUNCION EXPONENCIAL

La función exponencial, es conocida formalmente como la función real ex, donde e es el número de Euler, aproximadamente 2.71828...; esta función tiene por dominio de definición el conjunto de los números reales, y tiene la particularidad de que su derivada es la misma función. Se denota equivalentemente como f(x)=ex o exp(x), donde e es la base de los logaritmos naturales y corresponde a la función inversa del logaritmo natural.

En términos mucho más generales, una función real E(x) se dice que es del tipo exponencial en base a si tiene la forma




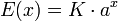
siendo a, K ∈ R números reales, con a > 0. Así pues, se obtiene un abanico de exponenciales, todas ellas similares, que dependen de la base a que utilicen.

Funciones exponenciales

Gráfica de Funciones exponenciales

FUNCION LOGARITMO

El logaritmo de un número —en una base de logaritmo determinada— es el exponente al cual hay que elevar la base para obtener dicho número. Por ejemplo, el logaritmo de 1000 en base 10 es 3, porque 1000 es igual a 10 a la potencia 3: 1000 = 103 = 10×10×10.

De la misma manera que la operación opuesta de la suma es la resta y la de la multiplicación la división, el cálculo de logaritmos es la operación inversa a la exponenciación de la base del logaritmo.

Para representar la operación de logaritmo en una determinada base se escribe la abreviatura log y como subíndice la base y después el número resultante del que deseamos hallar el logaritmo. Por ejemplo, 35=243 luego log3243=5. Cuando se sobreentiende la base, se puede omitir.

Los logaritmos fueron introducidos por John Napiera principios del siglo XVII como un medio de simplificación de los cálculos. Estos fueron prontamente adoptados por científicos, ingenieros, banqueros y otros para realizar operaciones fácil y rápidamente, usando reglas de cálculo y tablas de logaritmos. Estos dispositivos se basan en el hecho más importante — por derecho propio — que el logaritmo de un producto es la suma de los logaritmos de los factores:

La noción actual de los logaritmos viene de Leonhard Euler, quien conectó estos con la función exponencial en el siglo XVIII

FUNCION LOGARITMICA

Para justificar la definición de logaritmos, es necesario mostrar que la ecuación

tiene una solución x y que esta solución es única, provista de que y es positivo y que b es positivo y distinto de 1. Una demostración de este hecho requiere del teorema del valor intermedio del cálculo elemental.3 Este teorema establece que una función continua que produce dos valores m y n también produce cualquier valor que se encuentre entre m y n. Una función es continua si esta no «salta», esto es, si su gráfico puede ser escrito sin levantar el lápiz del papel.

Esta propiedad se puede demostrar que se cumple para la función f(x) = bx. Puesto que f toma arbitrariamente valores grandes positivos y valores pequeños positivos, cualquier número y > 0 que se encuentra entre f(x0) y f(x1) para un adecuado x0 y x1. Por lo tanto, el teorema del valor intermedio asegura que la ecuación f(x) = y tiene una solución. Más aún, hay únicamente una solución para esta ecuación, puesto que la función f es estrictamente creciente (para b > 1), o estrictamente decreciente (para 0 < b < 1).4

La única solución x es el logaritmo de y en la base b, logb(y). La función que asigna a cada y su logaritmo se llama función logaritmo o función logarítmica (o logaritmo a secas).

Función inversa

Gráfica de la función logarítmica logb(x) (azul) se obtiene mediante reflexión del gráfico de la función bx (roja) sobre la línea diagonal (x = y).

La fórmula para el logaritmo de una potencia dice en particular que para cualquier número x,

En lenguaje llano, tomando la x-ésima potencia de b y luego elbase-b logaritmo se vuelve a obtener x. De modo contrario, dado un número positivo y, la fórmula

dice que tomando primero el logaritmo y después exponenciando se vuelve a obtener y. Así, las dos maneras posibles de combinar (o componer) logaritmos y exponenciales vuelve a dar el número original. Por lo tanto, el logaritmo en baseb es la función inversa de f(x) = bx.5
Las funciones inversas están íntimamente relacionadas con las funciones originales. Sus gráficos se corresponden el uno con el otro mediante el intercambio de las coordenadas x e y (o por reflexión sobre la línea diagonal x = y), como se muestra en la figura de la derecha: un punto (t, u = bt) sobre el gráfico de fproporciona un punto (u, t = logbu) sobre el gráfico del logaritmo y viceversa. Como consecuencia, logb(x)diverge a infinito (se hace más grande que cualquier número dado) si x tiende a infinito, siempre que b sea mayor que 1. En ese caso, logb(x) es un función creciente. Para b < 1, logb(x) tiende a menos infinito en lugar de a infinito. Cuando x se aproxima a cero, logb(x) tiende a menos infinito para b > 1 (a más infinito cuandob < 1, respectivamente)..

FUNCIONES PERIODICAS

Una función es periódica si los valores de la función se repiten conforme se añade a la variable independiente un determinado período, o sea:

donde P es el período.

De la misma manera, pero en un contexto físico, lasondas periódicas son aquellas ondas que muestran periodicidad respecto del tiempo,es decir, describen ciclos repetitivos. En una onda periódica se cumple:

donde el periodo propio fundamental , es la frecuencia de la componente fundamental de la onda periódica y un número entero.

Toda onda periódica es, por definición, una onda determinista, por cuanto puede ser descrita matemáticamente (mediante un modelo matemático).

La onda periódica más simple: una onda armónica. En este ejemplo, A=1, Ω=1 y θ=0.

Funciones seno y coseno

Las funciones seno y coseno tienen dos matices:
a) Se generan a partir de las coordenadas (x,y) de un punto en un circulo unitario r=1
b) Se genera a partir del cociente de las longitudes de los lados de un triángulo rectángulo, generados por definición, así:


el utilizar la definición de las funciones seno y coseno y el siguiente gráfico, donde se analiza el triángulo generado del centro del circulo al punto sobre el circulo cuyo radio esr=1

Nota es importante considerar que:
p radianes = 180 grados
1 radián = (180 / p) grados
1 grado = (p / 180) radianes





Esto nos genera la gráfica:

De manera análoga se puede generar la función coseno

RAZONES TRIGONOMETRICAS

El triángulo ABC es un triángulo rectángulo en C; lo usaremos para definir las razones seno, coseno y tangente, del ángulo , correspondiente al vértice A, situado en el centro de la circunferencia.
El seno (abreviado como sen, o sin por llamarse "sĭnus" en latín) es la razón entre el cateto opuesto sobre la hipotenusa

.

El coseno (abreviado como cos) es la razón entre el cateto adyacente sobre la hipotenusa,

La tangente (abreviado como tan o tg) es la razón entre el cateto opuesto sobre el cateto adyacente,

GRÁFICO DE LAS FUNCIONES SENO Y COSENO

Consideramos como “Gráficas de las funciones (Seno, Coseno, Tangente)” al comportamiento que van presentando dichas funciones previamente mencionadas a través del recorrido de un conjunto de valores entrantes llamado así mismo (Dominio) y su conjunto de valores de salientes (Rango).

Estos dos valores (Entrante, Saliente) es lo que conforma en un momento dado una secuencia de elementos (Coordenada) a la cual le otorgamos una interpetación gráfica como elementos de un (Sistema de coordenadas cartesianas) formando una gráfica, que es lo que generalmente observamos ya como la (Gráfica de la función).

Como se muestra, para los casos de (Seno, Coseno, Tangente):

SENO (GRAFICA)



Comúnmente hacemos referencia a un (sistema de coordenadas cartesianas) como un conjunto de dos ejes graduados que se intersectan y nos permiten establecer una posición en base a esa graduación, como se observa en la imagen superior de la función.

COSENO (GRAFICA)



TANGENTE (GRAFICA)



Dichos gráficos, son parte de las relaciones conocidas como:



Los cuales son construidos a base de métodos de tabulación o conocimiento de periodos. Claro en lo que se refiere al trazado a mano por supuesto.

¿Para qué se utiliza el teorema seno y coseno en la vida cotidiana u otras actividades?

Después de saber sus leyes, como resolverlo y solucionar problemas¿Para que la utilizamos en la vida cotidiana?

La utilidad más importante de las funciones trigonométricas tiene que ver con la geometría, y el cálculo de ángulos, que se usan en el diseño y la fabricación de innumerables objetos, además de tener su utilidad en infinitas aplicaciones prácticas de la vida cotidiana. También se usa mucho en la construcción de viviendas, y en general cuando deseas saber la medida de un ángulo a partir de otros datos

tutorial de mate

tutorial de mate 2